Question

Find the coordinates of the reflection: B (5, 4) is reflected over the line x=1

B'=?
a
(6,4)
(6,5)
(-3,4)
(4,4)

Answer 1

The coordinates of point B' are (-3, 4) ⇒ C

Explanation:

If the point (x, y) reflected across the line x = a, then a is the x-coordinate of the midpoint of the segment joining the point and its image

∵ The coordinates of point B are (5, 4)

∴ x = 5 and y = 4

∵ The point B is reflected over the line x = 1

→ From the rule above

∴ a = 1

∵ The rule of the midpoint is M = (
`(x1+x2)/(2)` ,
`(y1+y2)/(2)`)

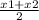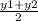→ The point B is (x1, y1) and the point B' is (x2, y2)

∵ a is the x-coordinate of the midpoint of segment BB'

∴ a =
`(x1+x2)/(2)`

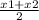
∵ x1 = 5 and x2 = x

→ Substitute the value of a, x1 and x2 in the rule above

∴ 1 =
`(5+x)/(2)`

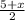
→ Multiply both sides by 2

∵ 2 = 5 + x

→ Subtract 5 from both sides

∴ 2 - 5 = 5 - 5 + x

∴ -3 = x

∴ The x-coordinate of B' = -3

→ y-coordinate of B' = y-coordinate of B because the reflection across

x = a does not change the y-coordinate

∴ y-coordinate of B' = 4

∴ The coordinates of point B' are (-3, 4)