Question

Which quadrilateral is a parallelogram

Answer 1

they are both quadrilatersand they are both parallelograms

Answer 2

III figure

Explanation:

Parallelogram:It is a figure of four sides.The opposite sides of parallelogram are equal and parallel.

Properties of parallelogram:

1.Opposite angles are equal.

2.Opposite sides are equal and parallel.

3.Sum of interior angles on the same side is equal to 180 degrees.

4.Diagonals of parallelogram bisect to each other.

When sum of interior angles on the same side is equal to 180 degrees.Then, the sides are parallel.

When one pair of opposite sides is parallel then, the quadrilateral is a parallelogram.

In I figure:

Sum of interior angles=
`78+108=186^(\circ)`

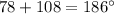
Sum of interior angles=
`\\eq 180^(\circ)`

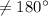
Side AC is not parallel to side BD.

Hence, it is not a parallelogram .

In II figure:

Sum of interior angles=
`113+57=170^(\circ)\\eq 180^(\circ)`

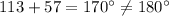
Therefore, side AC is not parallel to side BD.

Hence, it is not a parallelogram .

In III figure:

Sum of interior angles=
`126+54=180^(\circ)`

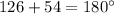
Therefore, side AC is parallel to side BD.

Hence, quadrilateral ABCD is a parallelogram.

In IV figure:

Sum of interior angles=
`60+110=170^(\circ)\\eq 180^(\circ)`

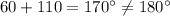
Therefore, side AB is not parallel to side CD.

Hence, quadrilateral ABCD is not a parallelogram.