Answer:
The line passing through points (0,3) and (1.5,0) . Line through (0,2) and (4,0).
Explanation:
We are given that two equations
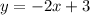 ...(I equation )
...(I equation )
 ....(II equation)
....(II equation)
We have to find the the graph of the given system
We solve first I equation
Substitute x=0 in equation I then we get
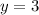
Now, we substituting y= 0 then we get
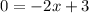

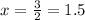

Hence, the line
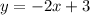 passing through the points (0,3) and (1.5,0).
passing through the points (0,3) and (1.5,0).
We are solving equation II
Substitute x= 0 in II equation
Then we get
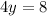
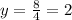

Now, we substituting y=0 then we get
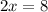
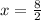
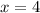
Therefore, the equation
 is passing through the points (0,2) and (4,0).
is passing through the points (0,2) and (4,0).
But any option does not match.