Question

Multiplying a trinomial by a trinomial follows the same steps as multiplying a binomial by a trinomial. Determine the degree and maximum possible number of terms for the product of these trinomials: (x2 + x + 2)(x2 – 2x + 3). Explain how you arrived at your answer.

ANSWER- Multiplying a trinomial by a trinomial follows the same steps as multiplying a binomial by a trinomial. Determine the degree and maximum possible number of terms for the product of these trinomials: (x2 + x + 2)(x2 – 2x + 3). Explain how you arrived at your answer.

Answer 1

To determine the degree of the product of the given trinomials, you would multiply the term with the highest degree of each trinomial together. Both trinomials are degree 2, and when you multiply x2 by x2, you add the exponents to get x4. Thus, the degree of the product is 4. If the product is degree 4, and there is only one variable, the maximum number of terms is 5. There can be an x4 term, an x3 term, an x2 term, an x term, and a constant term.

Explanation:

edge 2022

Answer 2

The degree of polynomial is equal to 4

The maximum number of terms is equal to 5.

Explanation:

Given the trinomials we have to find the degree and maximum possible number of terms for the product of these trinomials.

`(x^2+x+2)(x^2-2x+3)`

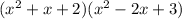
By distributive property,

`x^2(x^2-2x+3)+x(x^2-2x+3)+2(x^2-2x+3)`

`(x^4-2x^3+3x^2)+(x^3-2x^2+3x)+(2x^2-4x+6)`

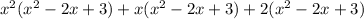
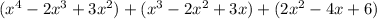
Grouping like terms

`x^4+(-2+1)x^3+(3-2+2)x^2+(3-4)x+6`

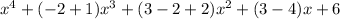
Adding terms of same power

`x^4-x^3+3x^2-x+6`

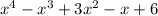
Hence, The degree of polynomial is equal to 4

The maximum number of terms is equal to 5.