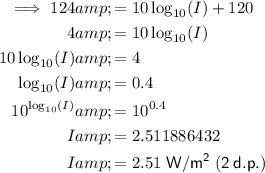Answer:
(a) D = 72.05 dB (2 d.p.)
(b) I = 2.51 W/m² (2 d.p.)
Explanation:
Given function:
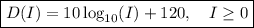
where:
- D is the sound intensity level (in dB).
- I is the sound intensity (in W/m²).
Part (a)
Given:
Substitute the given value of I into the given function and solve for D:

Part (b)
Given:
Substitute the given value of D into the given function and solve for I: