Question

What best describes an impulse acting on an object?

A) the net force on an object divided by the time of impact
B) the velocity of an object divided by its mass
C) the product of an object's mass and the time of force impact
D) the product of an object's mass and its change in velocity

Answer 1

D) the product of an object's mass and its change in velocity

Step-by-step explanation:

The impulse is defined as:

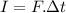`I = F . \Delta t` (1)

Where I is the impulse, F is the force and t is the time whereby the force will be applied on the object.

By using Newton's second law, the impulse can be related with the mass and the change in velocity as a consequence of the acting force:

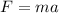`F = ma` (2)

Where F is the force, m is the mass and a is the acceleration.

The acceleration can be determined using the equations for a Uniformly Accelerated Rectilinear Motion:

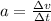`a = (\Delta v)/(\Delta t)` (3)

Where
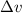`\Delta v` is the change in velocity (
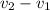`v_(2) - v_(1)`) and
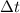`\Delta t` is the interval of time (
`t_(2) - t_(1)`)

Remember that the acceleration is defined as the change in velocity in an interval of time.

By replacing equation (3) in equation (2) it is gotten:

`F = m(\Delta v)/(\Delta t)`

`F . \Delta t = m\Delta v`

`F . \Delta t = m(v_(2) - v_(1))`

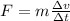
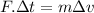
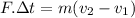
But
`F . \Delta t` is the impulse according with equation (1), therefore:

`I = m(v_(2) - v_(1))`

So what best describes an impulse acting on an object is the product of an object's mass and its change in velocity.

Answer 2

option (D)

Step-by-step explanation:

If a large force acting on a body for a very small interval of time, it is called impulse.

Impulse is a vector quantity. its SI unit is kg m/s.

The formula of impulse is given by

Impulse = Force x Δ t = change in momentum.