Question

what is the most precise name for quadrilateral abcd with vertices a(-5, -1) b(-5, 3) c(-2, 3) d(-2, -1)

Answer 1

check the picture below.

is a parallelogram, it has two pairs of sides that are parallel.

hmmm is not a square, since is a 3x4, so all sides aren't equal.

is a quadrilateral, it has four sides alright.

though is not a square, it does have 4 right-angles at its corners... that means that is a rectangle, besides being a parallelogram.

Answer 2

1st Option is correct.

Explanation:

Given:

Vertices of the quadrilateral ABCD.

A( -5 , -1 ) , B( -5 , 3 ) , C( -2 , 3 ) , D( -2 , -1 )

To find: Name of the Quadrilateral.

We use Distance formula to find the length of the sides and diagonal of the Quadrilateral.

Distance between two point =
`√((x_2-x_1)^2+(y_2-y_1)^2)`

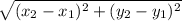
Length of Side AB
`=√((-5-(-5))^2+(-1-3)^2)=√((0)^2+(-4)^2)=√(0+16)=4`

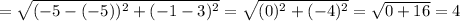
Length of Side CB
`=√((-2-(-5))^2+(3-3)^2)=√((-2+5)^2+(0)^2)=√(9+0)=3`

Length of Side CD
`=√((-2-(-2))^2+(-1-3)^2)=√((0)^2+(-4)^2)=√(0+16)=4`

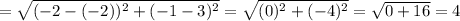
Length of Side AD
`=√((-2-(-5))^2+(-1-(-1))^2)=√((3)^2+(0)^2)=√(9+0)=3`

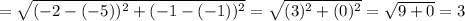
Length of the Diagonal AC
`=√((-2-(-5))^2+(3-(-1))^2)=√((3)^2+(4)^2)=√(9+16)=5`

Length of the Diagonal BD
`=√((-2-(-5))^2+(-1-3)^2)=√((3)^2+(-4)^2)=√(9+16)=5`

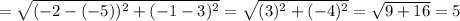
So, Opposite side of the Quadrilateral are Equal that is AB = CD = 4 unit and CB = AD = 3 unit

Also, Diagonals are equal that is AC = BD = 5 unit

⇒ Quadrilateral is a RECTANGLE.

Therefore, 1st Option is correct.