Question

Can someone help me understand how to do these please

Answer 1

1)

you can think of the cup's sleeve as a cylinder with say a height of 4 and a diameter of 5. Now, if the diameter is 5 inches, the radius is half that, or 2.5,


`\bf \textit{total surface area of a cylinder}\\\\ s=2\pi r(h+r)\quad \begin{cases} r=2.5\\ h=4 \end{cases}\implies s=2\pi (2.5)(4+2.5) \\\\\\ s=5\pi (6.5)\implies s=32.5\pi`

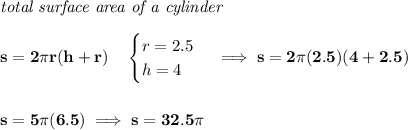
2)

same here, you can think of the tire as a cylinder, since it's a cylindrical tire, with a height of 8 and a diameter of 29, therefore a radius of 14.5,


`\bf \textit{total surface area of a cylinder}\\\\ s=2\pi r(h+r)\quad \begin{cases} r=14.5\\ h=8 \end{cases}\implies s=2\pi (14.5)(8+14.5) \\\\\\ s=29\pi (22.5)\implies s=652.5\pi`

now, that's how much spaces it covers one time only, so 5 times around is just 5 times that much.

3)

same goes for the mugs,


`\bf \textit{total surface area of a cylinder}\\\\ s=2\pi r(h+r)\quad \begin{cases} r=2\\ h=3.75 \end{cases}\implies s=2\pi (2)(3.75+2) \\\\\\ s=4\pi (5.75)\implies s=\stackrel{one~mug}{23\pi }\qquad\qquad \stackrel{4~mugs}{4\cdot 23\pi }`

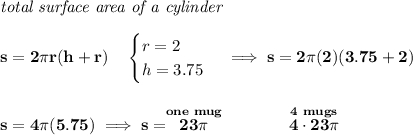
4)

and the same goes for the can of peas, which is also a cylinder,


a)


`\bf \textit{total surface area of a cylinder}\\\\ s=2\pi r(h+r)\quad \begin{cases} r=3.8\\ h=10 \end{cases}\implies s=2\pi (3.8)(10+3.8) \\\\\\ s=7.6\pi (13.8)\implies s=101.08\pi`

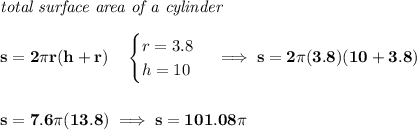
b)

the label is only the sides, and thus only the lateral area,


`\bf \textit{\underline{lateral} surface area of a cylinder}\\\\ s=2\pi rh\quad \begin{cases} r=3.8\\ h=10 \end{cases}\implies s=2\pi (3.8)(10)\implies s=76\pi`