Question

A two-digit number is 3 more than 4 times the sum of its digits. If 18 is added to the number, the digits are reversed. Find the number.​

Answer 1

Let the required number be ab.

Sum of digits = a + b ........ ( 1 )

10 a + b = 4 ( a + b )

10 a + b + 18 = 10 b + a

=> 9 a + 18 = 9 b

=> a + 2 = b

10 a + a + 2 = 4 ( a + a + 2 )

=> 11 a + 2 = 8 a + 8

=> 3 a = 6

=> a = 3

=> a + 2 = 5

=>ab = 35......... [ A ]

So the number becomes 35.

ANSWER :

The original number is 35.

hope it helps you

Answer 2

Given :

• (two-digit number) = 3 + 4(sum of its digits)

• (two-digit number) + 18 = Digit gets reverse

To Find :

• The number.

Concept :

-We will first assume the number on one's place be
`x` and ten's place be
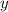`y` [why? because the given conditions are about the digits of number]

-Two-digit number then formed will be 10y + x and its reverse will be 10x + y[why? well let's take an example like a number 42. This number can be written in expanded form as 10×4+2×1 here 4 is number at ten's place (y) and 2 at one's place(x) It's reverse will be 24 it can be written in expanded form as 10×2+4×1 here 2 is number at ten's place (y) and 4 at one's place(x)]

-Then we will use given conditions to form the equation and will solve the equations to get the answer.

So now let's get started with our solution! :D

Solution :

Let the one's and ten's digit of the number be
`x` and
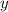`y` respectively.

According to first condition,

=> (10y + x) = 3 + 4(x + y)

=> 10y + x = 3 + 4x + 4y

=> 10y - 4y = 3 + 4x - x

=> 6y = 3 + 3x

`\implies \sf (6y)/(3) = (3)/(3) + (3x)/(3)`

=> 2y - 1 = x ___(equation 1)

According to second condition,

=> (10y + x) + 18 = 10x + y

=> 10y - y + 18 = 10x - x

=> 9y + 18 = 9x

`\implies \sf (9y)/(9) + (18)/(9) = (9x)/(9)`

=> y + 2 = x ___(equation 2)

Solving equation 1 and 2

y + 2 = x (equation 2)

y + 2 = 2y - 1 [From equation 1]

3 = 2y - y

3 = y (ten's place)

Now put value of y = 3 in equation 2

y + 2 = x (equation 2)

3 + 2 = x

5 = x (one's place)

So, the number formed is 35.