Question

In the coordinate plane, a circle has center (2,−3) and passes through the point (5,0). what is the area of the circle?

Answer 1

Find the radius (or you can find the square of the radius)
the general equation for a circle is
(x - a)² + (y - b)² = r²
with (a,b) as the center, and (x,y) is one of the points

plug in the numbers to the equation to find the value of r
(x - a)² + (y - b)² = r²
(5 - 2)² + (0 - (-3))² = r²
3² + (0 + 3)² = r²
3² + 3² = r²
2(3²) = r²
r² = 2(3²)
r² = 2(9)
r² = 18

Find the area of the circle
a = π × r²
a = 3,14 × 18
a = 56.52

The area of the circle is 56.52 square unit

Answer 2

Answer: The area of the circle is 56.57 sq. units.

Step-by-step explanation: We are given to find the area of a circle that has center (2, -3) and passes through the point (5, 0).

We know that the area of a circle with radius 'r' units is given by

`A=\pi r^2.`

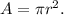
The standard equation of a circle with center (h, k) and radius 'r' units is given by

`(x-h)^2+(y-k)^2=r^2~~~~~~~~~~~~~~~~(i)`

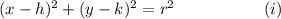
For the given circle, we have

center, (h, k) = (2, -3). So, equation (i) becomes

`(x-2)^2+(y+3)^2=r^2.`

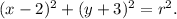
Since the circle passes through the point (5, 0), so we get

`(5-2)^2+(0+3)^2=r^2\\\\\Rightarrow r^2=3^3+3^2\\\\\Rightarrow r^2=18\\\\\Rightarrow r=3\sqrt2.`

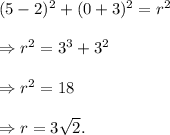
So, the radius of the circle is 3√2 units.

Therefore, the area of the circle will be

`A\\\\=\pi r^2\\\\=(22)/(7)* (3\sqrt2)^2\\\\=(22)/(7)* 18\\\\=56.57~\textup{sq. units.}`

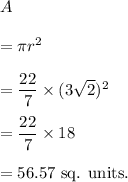
Thus, the area of the circle is 56.57 sq. units.