Question

If vx = 7.50 units and vy = -6.10 units, determine (a)the magnitude and (b)direction of v⃗ .

Answer 1

(a) v= 9.66 units

(b) α = -39.12°

α = 39.12° below the positive axis of the x

Step-by-step explanation:

Data

vx = 7.50 units

vy = -6.10 units

(a)Calculation of the magnitude of v

`v=\sqrt{(v_(x) )^(2) +(v_(y)) ^(2) }`

`v= \sqrt{(7.5)^(2)+(-6.1)^(2)  }`

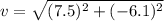
v= 9.66 units

(b)Calculation of the direction of v

`\alpha = tan^(-1)( (v_(y) )/(v_(x) ) )`

`\alpha = tan^(-1)( ( -6.1 )/(7.5 ) )`

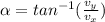
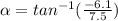
α = -39.12°

α = 39.12° below the positive axis

Answer 2

The magnitude of a vector is defined as the square root of its components squared.
We have then that the magnitude is:
v = root ((7.50) ^ 2 + (- 6.10) ^ 2)
v = 9.67 units
The direction of the vector is:
x = Atan (vy / vx)
x = Atan ((- 6.10) / (7.50))
x = -39.12 degrees (measured from the x axis)
answer:
v = 9.67 units
x = -39.12 degrees (measured from the x axis)