Answer:
Product of cube root of :
![\sqrt[3]{16x^7} * \sqrt[3]{12x^9}](https://img.qammunity.org/2019/formulas/mathematics/college/961nic2m2b4njlmqt7qqce0tc6499yugzu.png)
First simplify :
![\sqrt[3]{16x^7}](https://img.qammunity.org/2019/formulas/mathematics/college/h6vzgpmce0v4r2k4o7jbusklk2lzsouz92.png)
Factor: One of two or more expressions that are multiplied together to get a product
then, we can write it as:
![\sqrt[3]{2 \cdot 8 x^7}](https://img.qammunity.org/2019/formulas/mathematics/college/32nw0huw9f4bge6ygzm04bradl54aovetm.png) ,
,
Rewrite 8 as
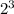 and
and
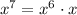
![\sqrt[3]{2\cdot 2^3 \cdot x^6 \cdot x}](https://img.qammunity.org/2019/formulas/mathematics/college/86bj72g47gso1dycqhbhj2xwib5vvsssn4.png) or
or
![\sqrt[3]{2\cdot 2^3 \cdot (x^2)^3 \cdot x}](https://img.qammunity.org/2019/formulas/mathematics/college/ln239gt8cdzwe23azihhdtt5kt9nb577e7.png) [∵
[∵
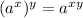 ]
]
or
![\sqrt[3]{2^3 \cdot (x^2)^3 \cdot 2\cdot x}](https://img.qammunity.org/2019/formulas/mathematics/college/3vyt38ywpi5nj43sybhtiy8sltbpmtf9qg.png)
or
![2 \cdot x^2\sqrt[3]{2\cdot x}](https://img.qammunity.org/2019/formulas/mathematics/college/wp8wonwlb11f94yrwxztyafbil60kuid1w.png) [∵
[∵
![\sqrt[3]{a^3} =a](https://img.qammunity.org/2019/formulas/mathematics/college/qi6we2km34o1lzc0nmdd99ulfsjdmgu5w0.png) ]
]
Similarly, we simplify for
![\sqrt[3]{12 x^9}](https://img.qammunity.org/2019/formulas/mathematics/college/zfkbqgh5657hq7snas8h9w1a25zc4whypg.png)
Then, we can write it as
![\sqrt[3]{12\cdot (x^3)^3}](https://img.qammunity.org/2019/formulas/mathematics/college/y00j7pq1sk4r7rdrt071jo5eckmdtzlpiy.png) or
or
![x^3 \cdot \sqrt[3]{12}](https://img.qammunity.org/2019/formulas/mathematics/college/68z3z5bfmr6e7ys7tjm1ae8ghgodxa9x0z.png)
Use :
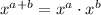 ,
,
![\sqrt[3]{a} \cdot\sqrt[3]{b} = \sqrt[3]{a \cdot b}](https://img.qammunity.org/2019/formulas/mathematics/college/iva9juoulz663i4uo97nsjyvfe661q3at0.png)
Now,
![\sqrt[3]{16x^7} * \sqrt[3]{12x^9}](https://img.qammunity.org/2019/formulas/mathematics/college/961nic2m2b4njlmqt7qqce0tc6499yugzu.png) =
=
![2 \cdot x^2\sqrt[3]{2\cdot x} * x^3 \cdot \sqrt[3]{12}](https://img.qammunity.org/2019/formulas/mathematics/college/tq62ubgg13rkri54va6v43z03yf2vkztsf.png)
=
![2x^2 \cdot x^3 \sqrt[3]{2x} \cdot \sqrt[3]{12}](https://img.qammunity.org/2019/formulas/mathematics/college/q2rknpymnizul57d6rpjv28r601zs2y3mb.png)
=
![2 x^5\cdot \sqrt[3]{2x \cdot 12}](https://img.qammunity.org/2019/formulas/mathematics/college/hm8azr85baj6r6fyzratbxi2etwbhcpdra.png) or
or
![2x^5 \cdot \sqrt[3]{24 x}](https://img.qammunity.org/2019/formulas/mathematics/college/q3rk6yypvbmggig37bldj0p8dippg9au48.png)
=
![2x^5 \cdot \sqrt[3]{8 \cdot 3x}](https://img.qammunity.org/2019/formulas/mathematics/college/icaohy7jus61g0tmw99uy7v639rkn4e99j.png) or
or
![2 x^5 \cdot \sqrt[3]{2^3 \cdot 3 \cdot x}](https://img.qammunity.org/2019/formulas/mathematics/college/b1wttnqdzmbio8ptmsmrzq5r6la82ygu4r.png)
=
![2x^5 \cdot 2 \sqrt[3]{3x}](https://img.qammunity.org/2019/formulas/mathematics/college/j3z7o6y66jjs6pq8i1yimtk3luplc5ds9e.png) =
=
![4 x^5 \cdot \sqrt[3]{3x}](https://img.qammunity.org/2019/formulas/mathematics/college/jm0oiv1hhgzln9sstkgljfs5aksiy33h88.png)
therefore, the product of
![\sqrt[3]{16x^7} * \sqrt[3]{12x^9}](https://img.qammunity.org/2019/formulas/mathematics/college/961nic2m2b4njlmqt7qqce0tc6499yugzu.png) is,
is,
![4 x^5 \cdot \sqrt[3]{3x}](https://img.qammunity.org/2019/formulas/mathematics/college/jm0oiv1hhgzln9sstkgljfs5aksiy33h88.png)