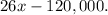Question

1. A rectangle has an area given by A=x^2+5x+6. Find expressions for the possible lengths and width of the rectangle.

2. The profits of a company are found by subtracting the company's costs from it's revenue. If a company's cost can be modeled by 14x+120,000 and it's revenue can be modeled by 40x-0.000x^2, what is the expression for the profit?

Answer 1

1.
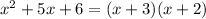
`x^2+5x+6 = (x+3)(x+2)`, which implies that the sides could be
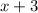
`x+3` and
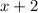
`x+2`. (There are theoretically an infinite number of side-lengths, though--in general, for any polynomial or reciprocal of a polynomial
`P(x)`,
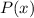
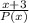
`(x+3)/(P(x))` and
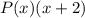
`P(x)(x+2)` is valid. However, the set provided makes the most sense.)

2. Profit is the difference between cost and revenue. For revenue,
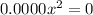
`0.0000x^2 = 0`, so revenue equals
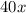
`40x`, so profit equals
`26x-120,000.`