Question

Frank just completed two tests. On his biology test, he earned a 55 while he earned a 70 on his chemistry test. The class average on the biology test was a 60 with a standard deviation of 10 while the class average on the chemistry test was an 80 with a standard deviation of 15. Relative to each class, which test did he do better on?

Answer 1

he did better in the biology test.

Answer 2

Since we cannot be 100% sure which test Frank did better on, we need to find a way to make the comparison doable. This can be done by converting Frank's score to the standard score (or also known as the z-score).

The z-score is calculated through the following formula:

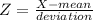
`Z= (X-mean)/(deviation)` where X is Frank's original score.

Converting Frank's scores to a standard score accounting for both the mean and standard deviation of the population who took the test will make the comparison possible.

We get the following z-scores after conversion:

`Z_(Bio)= (55-60)/(10) =-0.5`

`Z_(Chem)= (70-80)/(15) =-0.67`

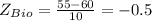
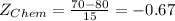
If you read up more on the concept of z-score, you may know that this score just means the amount of standard deviations a data falls with respect to the mean. Comparing Frank's two scores, we can see that they are both below the mean. However, it can be seen that Frank's z-score for his chemistry test is lower than his z-score for his biology test.

This suggests that Frank scored relatively poorer in chemistry than he did in biology.

ANSWER: Frank did better in his biology test.