Question

What would be the transformation?<3

Answer 1

`\bf ~~~~~~~~~~~~\textit{function transformations} \\\\\\ % templates f(x)= A( Bx+ C)+ D \\\\ ~~~~y= A( Bx+ C)+ D \\\\ f(x)= A√( Bx+ C)+ D \\\\ f(x)= A(\mathbb{R})^( Bx+ C)+ D \\\\ f(x)= A | B x+ C |+ D \\\\ --------------------`


`\bf \bullet \textit{ stretches or shrinks horizontally by } A\cdot B\\\\ \bullet \textit{ flips it upside-down if } A\textit{ is negative}\\ ~~~~~~\textit{reflection over the x-axis} \\\\ \bullet \textit{ flips it sideways if } B\textit{ is negative}\\ ~~~~~~\textit{reflection over the y-axis} \\\\`


`\bf \bullet \textit{ horizontal shift by }( C)/( B)\\ ~~~~~~if\ ( C)/( B)\textit{ is negative, to the right}\\\\ ~~~~~~if\ ( C)/( B)\textit{ is positive, to the left}\\\\ \bullet \textit{ vertical shift by } D\\ ~~~~~~if\ D\textit{ is negative, downwards}\\\\ ~~~~~~if\ D\textit{ is positive, upwards}\\\\`

now, with that template in mind, let's see,


`\bf y=\cfrac-{2}+1\implies y=-\cfrac{1}{2}|1x-8|+1\\\\\\ y=\stackrel{A}{-\cfrac{1}{2}}|\stackrel{B}{1}x\stackrel{C}{-8}|\stackrel{D}{+1}`

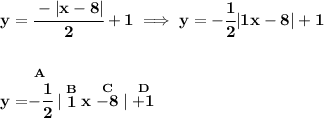
notice, first off A is negative, reflection over the x-axis.

A is also 1/2, not 1 as in the parent, 1/2 will expand the graph horizontally.

B is unchanged from the parent function as 1.

C is -8, therefore C/B is -8/1 or just -8, namely a horizontal shift to the right by that many units.

D is +1, so a vertical shift upwards of that much.