Answer:
65,535
Explanation:
This is a geometric progression with r = 4
Since 12/3 = 4
48/12 = 4
etc.
Sum of geometric series =

Where
r is common ratio and a is first term, n is the number of terms
If we mutiply 192 by 4, we get 768,
768 * 4 = 3072
3072 * 4 = 12,288
12,288 * 4 = 49,152
Thus, if we count, we see there are 8 terms, so n = 8
Now putting everything in the formula, we get:
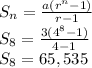
The sum is 65,535