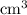Question

What is the volume of this pyramid?

Answer 1

Volume of a triangular pyramid=(1/3)Bh
B=base=area of the triangle located in the base=(1/2)(base)(height)=
=(9 cm)(15 cm)/2=67.5 cm²
height=32 cm

Volume=(1/3)/(67.5 cm²)(32 cm)=720 cm³

Answer: 720 cm³

Answer 2

Option A is correct

720
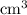`\text{cm}^3` is the volume of the pyramid

Explanation:

Volume of a triangular pyramids is given by:

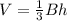`V = (1)/(3)Bh` ......[1]

where

V is the volume of the triangular pyramid

B is the base area

h is the height of the pyramids

From the given figure:

h = 32 cm

to find the Area of the base.

Use formula:

`B = (1)/(2)xy`

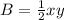
where x represents the width and y represents the height of the Base in the pyramids.

Here, x = 9 cm and y = 15 cm

then;

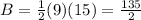`B = (1)/(2)(9)(15)=(135)/(2)` centimeter square.

Substitute the value of B in [1] we get;

`V = (1)/(3)\cdot (135)/(2) \cdot 32 = 45 \cdot 16`

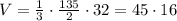
Simplify:

V = 720 centimeter cube

Therefore, the volume of the given pyramids is 720
`\text{cm}^3`