Question

Given a circle with radius of 2, which is the degree measure of an arc whose length is 1/2 pie ?

Answer 1

45 degrees

Explanation:

90 divided by 2 = 45.

Answer 2

Formula to find the arc length is:

`s=(\theta)/(360) 2\pi r`

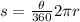
So, if we want to measure the central angle then it will be:

`\theta= (360s)/(2r\pi)`

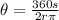
Where, s= arc length,

r = radius of the circle

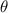`\theta`= central angle in degrees.

According to the given problem,
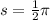`s=(1)/(2) \pi` and r = 2.

So, first step is to plug in these values in the above formula.

`\theta=(360*(1)/(2)\pi)/(2*2\pi)`

`=(360*(1)/(2))/(2*2)`

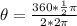
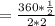
π has been cancel out from both top and bottom.

`=(180)/(4)`

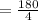
=45

So, measure of central angle is 45°.