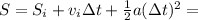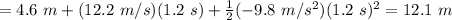Question

A ball is thrown straight up from the edge of a 15 foot balcony with initial velocity 40 feet/sec. how high will the ball travel?

Answer 1

Hello
The initial height of the ball is
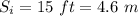
`S_i = 15~ft = 4.6~m`, while the initial velocity is
`v_i = 40ft/s = 12.2~m/s`.
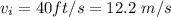
This is a uniformly accelerated motion, where the acceleration is the gravitational acceleration:
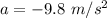
`a=-9.8~m/s^2`, where the negative sign means that the acceleration points downwards.
We can proceed in two steps:

1) First of all, we calculate the time the ball needs to reach the maximum height. At the point of maximum height, the velocity is zero:
`v_f = 0m/s`.
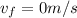
We can use the formula

`a= (v_f-v_i)/(\Delta t)`
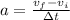
To find the time:

`\Delta t= (v_f-v_i)/(a) = 1.2 s`

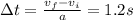
2) At this point, we can calculate the total height reached by the ball after this time, i.e. the maximum height:

`S=S_i+v_i \Delta t+ (1)/(2) a (\Delta t)^2 =`

`= 4.6~m+(12.2~m/s)(1.2~s)+ (1)/(2)(-9.8~m/s^2)(1.2~s)^2 = 12.1~m`