Question

If f(x)=5x-6 and g(x)=x^2-4x-8, find (f+g)(x)

a. (f+g)(x)=x^2-x-2
b. (f+g)(x)=6x^2-4x-14
c. (f+g)(x)=x^2+x-14
d. (f+g)(x)=x^2-9x-2

Answer 1

(f+g)(x)= f(x) + g(x) = 5x-6 + x^2-4x-8 = x^2+x-14

Answer 2

Option c -
`(f+g)(x)=x^2+x-14`

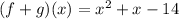
Explanation:

Given :
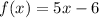`f(x)=5x-6` and
`g(x)=x^2-4x-8`

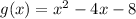
To find : The value of
`(f+g)(x)`?

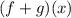Solution :

Step 1 - Write the expression in form,

`(f+g)(x)=f(x)+g(x)`

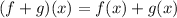
Step 2 - Substitute the value of f(x) and g(x),

`(f+g)(x)=5x-6+x^2-4x-8`

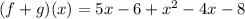
Step 3 - Solve by adding like terms,

`(f+g)(x)=x^2+x-14`

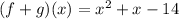
Therefore, The value of the expression is
`(f+g)(x)=x^2+x-14`

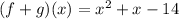
So, Option 'c' is correct.