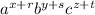Question

(a^xb^yc^z)(a^rb^sc^t) someone please help

Answer 1

If you're just supposed to expand, then start by grouping together terms of the same base.


`(a^xb^yc^z)(a^rb^sc^t)=(a^xa^r)(b^yb^s)(c^zc^t)`

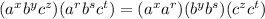
which is true since multiplication is commutative/associative. By definition of exponentiation, we have


`a^xa^r=a^(x+r)`

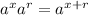
and the same goes for the remaining bases. So the fully simplified form of the expression above would be


`a^(x+r)b^(y+s)c^(z+t)`