Question

Use a table of values to find the solution to the equation ƒ(x ) = h(x ) where f(x)=1/x+1 and h(x ) = 2x + 3. Show your work

Answer 1

We have to use the table of values to find the solution to the equation:

f(x)=h(x)

Where
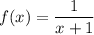`f(x)=(1)/(x+1)` and
`h(x)=2x+3`

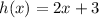
Now we make a table as:

x f(x) h(x)

0 1 3

0.5 0.666 4

1 0.5 5

2 0.333 7

-0.5 2 2

-1 ∞ 1

-1.5 -2 0

-2 -1 -1

Hence, from the set of values as in the table we could clearly observe that the points where f(x)=h(x) is at x= -0.5 and x=-2.

Also we could observe from the graph that the x-value of the point of intersection of the graphs of the function f(x) and h(x) are the solutions of f(x)=h(x).

Answer 2

f(x)=1/(x+1)

h(x ) = 2x + 3

I proceed to make the table, placing different values ​​of X until we get

f (x) = g (x) (see the attached table)

The solutions to this problem are (-0.5, 2) and (-2,-1)