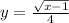Answer:
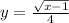
Explanation:
The given equation is
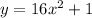
For this function to have an inverse, we must restrict the domain, say
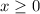
We interchange x and y to get,
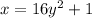
We now make y the subject to get;


We divide through by 16 to get;
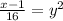
We now take the square root of both sides to get;
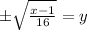
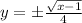
Since
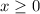 , the inverse function is
, the inverse function is