Question

Determine whether a triangle can be formed with the given side lengths. If so, use Heron's formula to find the area of the triangle a = 240 b = 121 c = 302

Answer 1

Yes, the triangle can be formed with the given side lengths and it would have an area of 13,724.27 squared units.

Explanation:

So first, yes, a triangle can be formed because the sum of the smaller sides is greater than the biggest side.

So first, Heron's formula consists on two parts:

`s=(a+b+c)/(2)`

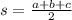
which is half of the perimeter of the triangle.

And the area formula itself:

`A=√(s(s-a)(s-b)(s-c))`

we know that a=240, b=121 and c=302

so we can start by calculating s.

`s=(a+b+c)/(2)=(240+121+302)/(2)=331.5`

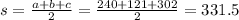
Once we got s, we can plug it into the given formula:

`A=√(s(s-a)(s-b)(s-c))`

which yields:

`A=√(331.5(331.5-240)(331.5-121)(331.5-302))`

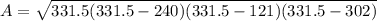
when solving the parenthesis we get:

`A=√(331.5(91.5)(210.5)(29.5))`

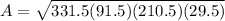
which simplifies to:

`A=√(188355689.4)`

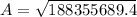
so the answer is:

A=13 724.27 squared units.