Question

What is the solution to the following system of equations?

Answer 1

substitute y =6x - 11 into -2x - 3y = -7

-2x - 3y = -7
-2x - 3(6x - 11) = -7
-2x - 18x + 33 = -7
-20x = -40
x = 2

y = 6(2) - 11
y = 12 -11
y = 1

answer
D. (2, 1)

Answer 2

The solution to the following system of equations is:

(2,1)

Explanation:

We have a system of equation as:

`y=6x-11--------------(1)`

and
`-2x-3y=-7------------(2)`

We solve following system of equation by the method of substitution.

We put the value of y in terms of x from equation (1) in equation (2)

`-2x-3(6x-11)=-7\\\\\\i.e.\\\\\\-2x-18x+33=-7\\\\\\i.e.\\\\\\-20x+33=-7\\\\\\i.e.\\\\\\20x=33+7\\\\\\i.e.\\\\\\20x=40\\\\\\i.e.\\\\\\x=2`

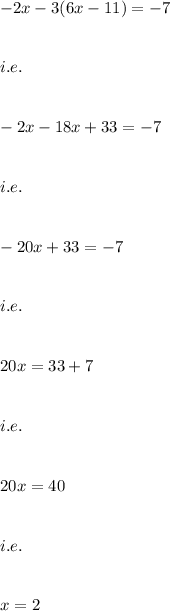
and now on putting the value of x back in equation (1) we get:

`y=6* 2-11\\\\\\y=12-11\\\\\\y=1`

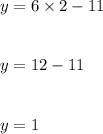
The solution is: (2,1)