Check the picture below.
the assumption being that the y-axis represents the water level more or less and the x-axis represents the minutes elapsed, we're also assuming this rate is constant, so it creates a straight-line on the cartesian plane.
We know that every 3 minutes pass, the level rises by 13 cm, let me reword that, we know that as the "rise" is 13, the "run" is 3, well, slope is rise/run, that simply gives us a slope of 13/3.
Now, we have another point on the line, (9 , y), whatever "y" might be, we know that the slope is y/x or rise/run, so we can say that
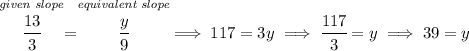
we know the slope is 13/3 or namely 13 cm every 3 mins, what about for just 1 minute? we can simply get their quotient, 13 ÷ 3 which is about 4.3 cms/min.