The original cost is $12000.
The value decreases by 6% in 12 months (1 year), so the cost after 12 months is
(1 - 0.06)*12000 = $11,280
Let k = the percent rate of decay each month
Let t = months
Model the value as
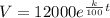
Therefore
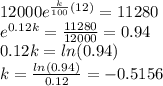
Answer: k = -0.5156%
Note that a different decay function will yield a slightly different answer.