Answer:
The area of the circle of spilled paint as a function of time is
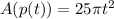 . The area of spilled paint after 2 minutes is 314.
. The area of spilled paint after 2 minutes is 314.
Explanation:
Consider the provided statement.
The paint flow can be expressed with the function
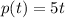 .
.
Where t represents time in minutes and p represents how far the paint is spreading.
The flowing paint is creating a circular pattern on the tile. The area of the pattern can be expressed as:
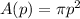 .
.
Part A: Find the area of the circle of spilled paint as a function of time, or A[p(t)].
Substitute
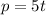 in
in
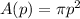 .
.
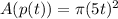
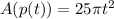
Hence, the area of the circle of spilled paint as a function of time is
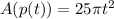 .
.
Part B: How large is the area of spilled paint after 2 minutes?
Substitute t = 2 in
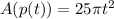 .
.
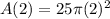
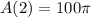
Use π = 3.14 in above equation.
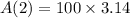
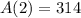
Hence, the area of spilled paint after 2 minutes is 314.