Question

Given that sin theta = 1/4, 0

Answer 1

Answer: cos(Θ) = (√15) / 4

Step-by-step explanation:

The question states:

1) sin(Θ) = 1/4

2) 0 < Θ < π / 2

3) find cos(Θ)

This is how you solve it.

1) Use the fundamental identity (in this part I use α instead of Θ, just for facility of wirting the symbols, but they mean the same for the case).


`(cos \alpha )^2 + (sin \alpha )^2 =1`

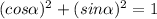
2) From which you can find:


`(cos \alpha )^2 = 1 - (sin \alpha )^2`

3) Replace sin(α) with 1/4

=>
`(cos \alpha )^2 = 1 - (1/4)^2 = 1 - 1/16 = 15/16`

=>
`cos \alpha =+/- √(15/16) = +/- (√(15) )/4`

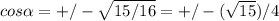
4) Given that the angle is in the first quadrant, you know that cosine is positive and the final answer is:

cos(Θ) =
`√(15) /4`.

And that is the answer.