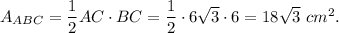Question

Given: ΔАВС, m∠ACB = 90°

CD ⊥ AB,

m∠ACD = 60°
BC = 6 cm
Find CD, Area of ΔABC

Answer 1

1. Length of CD
Considering Triangle CDB
Angle DCB = 30
Using trigonometric ratio
Cos θ = adjacent/hypotenuse
Cos 30 = CD/CB
Cos 30 = CD/6
CD = 6(Cos 30)
= 5.196 cm

2. The area of triangle ABC
area of Δ ABC = ares of Δ ACD + Area of DCB
Area of Δ DCB
= 1/2 × 3× 5.195
= 7.79 cm²
length of AD
Tan 60 = AD/5.196
AD= 8.999
≈ 9 cm
Area of of ADC
= 1/2 × 9 × 5.196
= 23.382 cm²
Therefore area of Δ ABC
= 23.382 cm² + 7.79 cm²
= 31.172 cm²

Answer 2

1. If m∠ACB=90° and m∠ACD=60°, then m∠BCD=30°. Consider right triangle BCD. BC is its hypotenuse.

The leg that lies opposite to the 30° angle is half of hypotenuse, then BD=3 cm.

By the Pythagorean theorem,

`CD^2+BD^2=BC^2,\\ \\CD^2+3^2=6^2,\\ \\CD^2=36-9=27,\\ \\CD=3√(3)\ cm.`

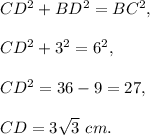
2. Consider right triangle ACD, m∠ACD=60°, then m∠CAD=90°-60°=30°. Thus, the leg CD is opposite to the hypotenuse AC and

`AC=2CD=2\cdot 3√(3)=6√(3)\ cm.`

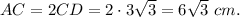
3. The area of ΔABC is

`A_(ABC)=(1)/(2)AC\cdot BC=(1)/(2)\cdot 6√(3)\cdot 6=18√(3)\ cm^2.`