Answer:
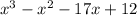
Explanation:
Write the polynomials one above the other to multiply them:
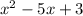
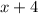
First Step
Multiply each element of
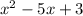 by 4:
by 4:
The result is:
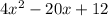 [1]
[1]
As it can be seen, only the coefficients are multiplied by 4, and when the operation involves multiplication with coefficients with different operators (+ or -), the following rules are crucial:
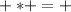


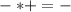
That is why 4 times -5 = -20, 4 times 1 = 4, and so 4 times 3 = 12.
Second Step
Multiply each element of
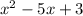 by x:
by x:
The same rules apply here, but including the addition of powers or exponents.
The result is:
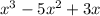 [2].
[2].
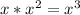 or
or
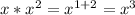
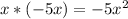
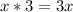
Third Step
Sum all similar terms of the previous results [1] and [2].
The result is:
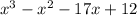 , because
, because
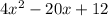
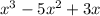
__________________________
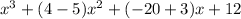
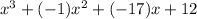
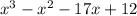 .
.