Question

The function M(s) = 225 + 0.65s represents the material cost of manufacturing gardening scissors when s scissors are produced. The function L(s) = 54 + 1.15s represents the labor cost for producing s scissors. Which expression correctly represents the manufacturing cost per scissors?

Answer choices are
A. 171 - 0.50s
B. 279 + 1.80s
C. 279 + 1.80s/s
D. 171-0.50s/s

Answer 1

Manufacturing Cost = M(s) + L(s)

Manufacturing Cost = 225 + 0.65s + 54 + 1.15s

Manufacturing Cost = 1.8s + 279

Answer 2

Option C. is the answer.

Explanation:

Function that represents the material cost is M(s) = 225 + 0.65s

and function representing the labor cost is L(s) = 54 + 1.15s

We have to find the expression for manufacturing cost.

Since Manufacturing cost = Labor cost + Material cost

= M(s) + L(s)

Now by replacing the values of M(s) and L(s)

Manufacturing cost = (225 + 0.65s) + (54 + 1.15s)

= (225 + 54) + (0.65s + 1.15s)

= 279 + 1.80s

Now manufacturing cost of one scissors =
`\frac{\text{Manufacturing cost}}{\text{Numbers of total scissors manufactured}}`

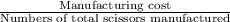
Here manufacturing cost is = 279 + 1.80s

and Number of scissors manufactured = s

So Manufacturing cost per scissors =
`(279+1.80s)/(s)`

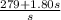
Therefore, Option C is the answer.