Question

The population of Whoville has been decreasing at a rate of 0.8% per year since Dr. Seuss passed away in 1991. If the population was 13,500 at the beginning of 2005, which expression gives its population at the end of 1998?

Answer 1

Well, if your asking from 2005 back to 1998... Starting from 13,500 take back 0.8% each year, in this case 7 years, it would be about 2831.

Answer 2

Using P(7) = 13500 in the expression
`P(t) = P(0)(0.992)^(t)`, we find that the population at the end of 1998 is given by the expression
`P(0) = (13500)/((0.992)^(7))` and it was of 14,281.

Explanation:

The population od Whoville in t years after 1998 is given by the following equation.

`P(t) = P(0)(1 - r)^(t)`

In which P(0) is the population in 1998 and r is the constant rate that it decreases, as a decimal.

The population of Whoville has been decreasing at a rate of 0.8% per year since Dr. Seuss passed away in 1991.

So
`r = 0.008`

Then

`P(t) = P(0)(1 - 0.008)^(t)`

`P(t) = P(0)(0.992)^(t)`

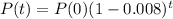
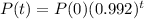
If the population was 13,500 at the beginning of 2005, which expression gives its population at the end of 1998?

2005 is 2005-1998 = 7 years after 1998. So p(7) = 13500. We have to find P(0).

`P(t) = P(0)(0.992)^(t)`

`13500 = P(0)(0.992)^(7)`

`P(0) = (13500)/((0.992)^(7))`

`P(0) = 14281`

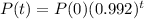
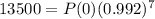
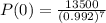
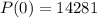
Using P(7) = 13500 in the expression
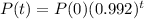`P(t) = P(0)(0.992)^(t)`, we find that the population at the end of 1998 is given by the expression
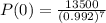`P(0) = (13500)/((0.992)^(7))` and it was of 14,281.