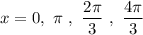Question

4. Simplify the expression. (6 points)

sine of x to the second power minus one divided by cosine of negative x


A) -sin x
B) cos x
C) sin x
D) -cos x

5. Find all solutions in the interval [0, 2π). (6 points)
sin2x + sin x = 0



A) x = 0, π, four pi divided by three , five pi divided by three
B) x = 0, π, pi divided by three , two pi divided by three
C) x = 0, π, pi divided by three , five pi divided by three
D) x = 0, π, three pi divided by two


PLEASE HELPP

Answer 1

4. Simplify the expression.
sine of x to the second power minus one divided by cosine of negative x

(1−sin2(x))/(sin(x)−csc(x))

sin2x+cos2x=1 1−sin2x=cos2x

cos2(x)/(sin(x)−csc(x)) csc(x)=1/sin(x) cos2(x)/(sin(x)− 1/sin(x))= cos2(x)/((sin2(x)− 1)/sin(x)) sin2(x)− 1=-cos2(x) cos2(x)/(( -cos2(x))/sin(x))
=-sin(x)
the answer is the letter a) -sin x

5. Find all solutions in the interval [0, 2π). (6 points)
sin2x + sin x = 0
using a graphical tool
the solutions x1=0 x2=pi x3=3pi/2
the answer is the letter D) x = 0, π, three pi divided by two

Answer 2

Answer with explanation:

Ques 4)

We are given a trignometric expression by:

`(\sin^2x-1)/(\cos (-x))`

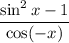
which could also be written as:

`=(-(1-\sin^2x))/(\cos x)`

since, we know that:

`\cos (-x)=\cos x`

Also,

`1-\sin^2 x=\cos^2 x`

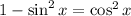
Hence, we get:

`(\sin^2x-1)/(\cos (-x))=(-\cos^2x)/(\cos x)\\\\\\(\sin^2x-1)/(\cos (-x))=-\cos x`

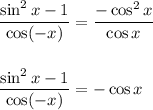
The correct option is:

D) -cos x

Ques 5)

We are asked to find the solution in the interval [0,2π) of the expression:

`\sin 2x+\sin x=0`

This expression could also be written as:

`2\sin x\cos x+\sin x=0\\\\i.e.\\\\\sin x(2\cos x+1)=0\\\\i.e.\\\\Either\ \sin x=0\ or\ 2\cos x+1=0`

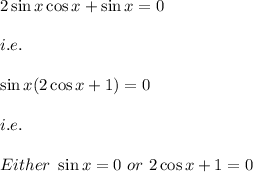
If

`\sin x=0`

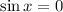
Then the possible values of x are:

`x=0,\pi`

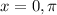
and if

`2\cos x+1=0\\\\i.e.\\\\\cosx=(-1)/(2)`

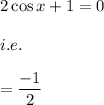
We know that the cosine function is negative in second and third quadrant and the possible values where x is negative is:

`x=(2\pi)/(3)\ ,\ x=(4\pi)/(3)`

Hence, all the solutions of the given expression that will lie in the given region is:

`x=0,\ \pi\ ,\ (2\pi)/(3)\ ,\ (4\pi)/(3)`