Question

If y varies jointly with x and z, and y = 200 when x = 8 and z = 10, what is x when y = 165 and z = 11?

What is the value of k?

Answer 1

The answer is 2.5

The next blank is 6

Answer 2

Joint variation states:

if y varies jointly with x and z

then the equation we get;

`y = k \cdot xz`

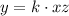
where, k is the constant of variation.

As per the statement:

If y varies jointly with x and z

Using above definition we have;

⇒
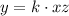`y = k \cdot xz` ....[1]

y = 200 when x = 8 and z = 10

Substitute these value in [1] to solve for k;

`200 = k \cdot 8 \cdot 10`

⇒
`200 = 80k`

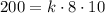
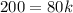
Divide both sides by 80 we have;

2.5 = k

or

k = 2.5

then we get an equation:

`y=2.5 \cdot xz`

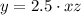
We have to find x when y = 165 and z = 11.

then;

`165 = 2.5 \cdot x \cdot 11`

⇒
`165 = 27.5x`

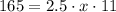
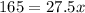
Divide both sides by 27.5 we have;

6 = x

or

x = 6

Therefore, the value of k = 2.5 and value of x is 6 when y = 165 and z = 11.