Answer:
The zeros of the given function
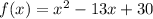 are 3 and 10
are 3 and 10
Explanation:
Given : Function
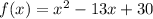
We have to find the zeros of the given function
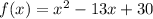
Consider the given function
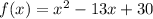
Since, we have to find the zeros of the given quadratic equation
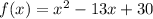
Put f(x) = 0
That is
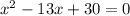
Now we will solve the above quadratic equation using middle term splitting method,
-13x can be written as -3x- 10x
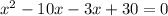
Taking x common from first two term and -3 common from last two terms, we have,
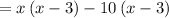
Taking (x- 10) common, we have,
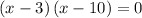
Using zero product rule,
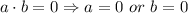
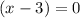 and
and
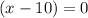
Simplify, we have,
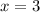 and
and
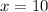
Thus, The zeros of the given function
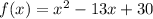 are 3 and 10.
are 3 and 10.