Question

If the couple has four children, what is the probability that at least one child will have g alactosemia?

Answer 1

This is more a biology question.
Galactosemia is an autosomal recessive genetic disease.
The probability depends on the prevalence (P) of carriers in the region.
It takes two carrier parents for a child to develop galactosemia, with probability of 1/4 because it is a recessive disease.
Therefore, under random conditions, the probability of both parents being carriers is P², and the probability that a particular child developing galactosemia is p=P²/4.

The probability of having NO (x=0) child out of n=4 developing the disease can be estimated by the binomial distribution,
P(X=x)=C(n,x)p^0(1-p)^n
which means, for p=P²/4, n=4, x=0
P(X=0)=C(4,0)p^0(1-p)^4

`=1*1*(1-p)^4`

`=(1-p)^4`

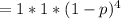
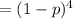
Consequently, the probability that at least one child will have galactosemia
P(X>0)=1-P(X=0)

`=1-(1-p)^4`

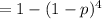
From the published incidence (p) of the disease in the US estimated to be between 1/30000 to 1/60000 [ ref. nih document # PMC4413015 ], we could use p=1/45000, giving
P(X>0)

`=1-(1-p)^4`

`=1-(1-1/45000)^4`

`=1-(4100260512149820001)/(4100625000000000000)`

`=(364487850179999)/(4100625000000000000)`

`=8.8886*10^(-5)`
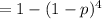
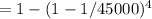
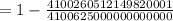
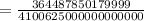
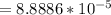
=0.0000889 (approximately)