Answer:
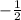
Explanation:
If we try direct substitution we get:

The radian
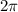 is a full rotation from 0 radians, in other words it's equivalent to 0 radians.
is a full rotation from 0 radians, in other words it's equivalent to 0 radians.
Using the unit circle as a reference you'll remember when the angle is 0 radians, the y-value is zero, so:
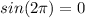
When the angle is:
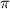 it's at a half rotation where the y-value is still zero on the unit circle.
it's at a half rotation where the y-value is still zero on the unit circle.
So you get the indeterminate form of:
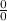
We can use L'Hôpital's rule which states:
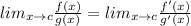 if the original limit is in indeterminate form such as the one above.
if the original limit is in indeterminate form such as the one above.
Taking the derivative of sin(x) we simply use the property that:
![(d)/(dx)[sin(x)]=cos(x)](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/1slcrumanoseu7sjbyi2.png)
For the sin(2x) we can use the chain rule which essentially states:
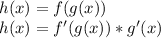
It deals with composite equations, and in this case we can represent the composite function as:
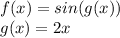
Using the chain rule we get:
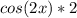
So now we have the limit:
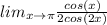
at pi radians the unit circle is at a half rotation where the x/y coordinates are:
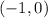
so cos(pi) = -1
at 2 * pi radians were basically back at 0 radians where the x/y coordinates are:
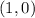
so cos(2 * pi) = 1
Now plugging in these values we get the fraction:
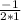 which just simplifies to:
which just simplifies to:
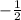 which turns out to be the limit!
which turns out to be the limit!