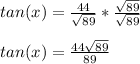Answer:
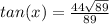
Explanation:
tan is defined as:
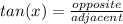
sin is defined as:
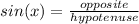
cos is defined as:
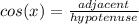
We can also define tan as:
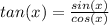
because plugging in the definitions of sin and cos in we get:
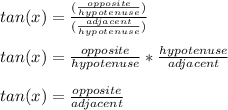
which you'll notice is the original definition of tan(x)
So using this definition of tan(x) we can use the givens sin(x) and cos(x) to find tan(x)
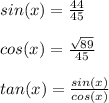
plugging in sin(x) and cos(x) we get:
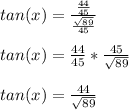
We usually don't like square roots in the denominator, and from here we want to rationalize the denominator which we do by removing the square root from the denominator.
We can do this by multiplying the fraction by:
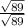 which doesn't change the value of the fraction since it simplifies to 1, but it gets rid of the square root in the denominator
which doesn't change the value of the fraction since it simplifies to 1, but it gets rid of the square root in the denominator