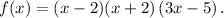Question

According to the rational root Theorum, which is a factor of the polynomial f(x) = 3x^3 -5x^2 - 12x + 20

Answer 1

In algebra, the rational root theorem states a constraint on rational solutions of a polynomial equation

`a_nx^n+a_(n-1)x^(n-1)+\dots +a_1x+a_0=0`

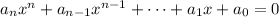
with integer coefficients. Solutions of the equation are roots of the polynomial on the left side of the equation.

If
`a_0` and
`a_n` are nonzero, then each rational solution x, when written as a fraction
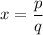`x=(p)/(q)` in lowest terms satisfies

• p is an integer factor of the constant term
  `a_0,`
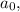
• q is an integer factor of the leading coefficient
  `a_n.`

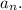
For the polynomial
`f(x) = 3x^3 -5x^2 - 12x + 20`,
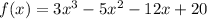`a_3=3,\ a_0=20.` Find factors of these coefficients:

• factors of
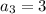  `a_3=3` are
  `\pm 1,\ \pm 3;`
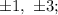
• factors of
  `a_0=20` are
  `\pm 1,\ \pm 2,\ \pm 4,\ \pm 5,\ \pm 10,\ \pm 20.`

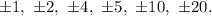
Therefore, possible roots are

`\pm 1,\ \pm 2,\ \pm 4,\ \pm 5,\ \pm 10,\ \pm 20,\ \pm (1)/(3), \ \pm (2)/(3),\ \pm (4)/(3),\ \pm (5)/(3),\ \pm (10)/(3),\ \pm (20)/(3).`

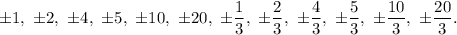
Check all that apply:

`f(2)=3\cdot 2^3 -5\cdot 2^2 - 12\cdot 2 + 20=3\cdot 8-5\cdot 4-24+20=24-20-24+20=0;`

`\\f(-2)=3\cdot (-2)^3 -5\cdot (-2)^2 - 12\cdot (-2) + 20=3\cdot (-8)-5\cdot 4+24+20=-24-20-24+20=0;`

`\\f\left((5)/(3)\right)=3\cdot \left((5)/(3)\right)^3 -5\cdot \left((5)/(3)\right)^2 - 12\cdot \left((5)/(3)\right) + 20=3\cdot \left((125)/(27)\right)-5\cdot \left((25)/(9)\right)-20+20=(125)/(9)-(125)/(9)=0.`

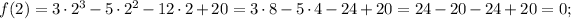
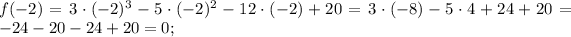
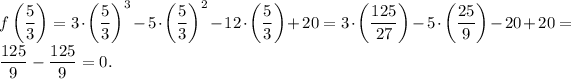
Then

`f(x) = 3x^3 -5x^2 - 12x + 20=3(x-2)(x+2)\left(x-(5)/(3)\right).`

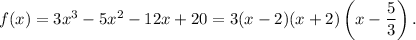
Answer: there are three possible factors

`(x-2),\ (x+2),\ \left(x-(5)/(3)\right).`

The last one can be rewritten as 3x-5, then
`f(x) =(x-2)(x+2)\left(3x-5\right).`

Answer 2

We will find the rational zeros of f(x) = 3x^3 -5x^2 - 12x + 20

1) Arrange in descending order: f(x) = 3x^3 -5x^2 - 12x + 20

2) write down the factors of the constant term, 20.
1,2, 4, 5, 10, 20 - these could all be the possible values of p.

3) write down the factors of the leading coefficient, 3.
1,3 - these are the possible values of q.
.
4) write down all the possible values of p/q. both positive and negative values must be written down. Simplify
1/1 ; 1/3 ; 2/1 ; 2/3 ; 4/1 ; 4/3 ; 5/1 ; 5/3 ; 10/1 ; 10/3 ; 20/1 ; 20/3
1 ; 0.33 ; 2 ; 0.67 ; 4 ; 1.33 ; 5 ; 1.67 ; 10 ; 3.33 ; 20 ; 6.67

5) use the simplified p/q in both positive and negative values in the synthetic division. Pls. see attachment for my synthetic division.

Based on my computations, a factor of the polynomial f(x) = 3x^3 -5x^2 - 12x + 20 is: x = -1.67 or x = -5/3

IF THESE ARE THE MISSING CHOICES:
A)2x + 1 B)2x - 1 C)3x+5 D)3x - 5.

MY ANSWER IS: D) 3x - 5.