Answer:
c. $21009.20
Explanation:
We are asked to find the principal amount of money that would be needed to deposited into an account earning 5.75% interest compounded annually in order for the accumulated value at the end of 25 years to be $85,000.
We will use compound interest formula to solve our given problem.
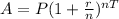 , where,
, where,
A = Final amount after T years,
P = Principal amount,
r = Interest rate in decimal form,
n = Number of times interest is compounded per year,
T = Time in years.
Let us convert our given interest rate in decimal form.
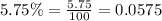
Upon substituting our given values in compound interest formula we will get,
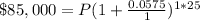
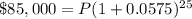
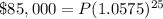
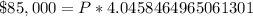
Let us divide both sides of our equation by 4.0458464965061301.
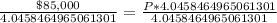
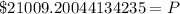
Upon rounding our answer to nearest hundredth we will get,
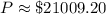
Therefore, an amount of $21009.20 should be deposited in the account and option 'c' is the correct choice.