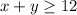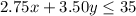Answer:
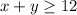
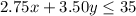
Explanation:
Let x represents the number of red roses and y represents the number of white roses.
Given : Javier is purchasing a bouquet of roses from a floral shop. He wants the bouquet to have at least 12 roses.
i.e. the required inequality for this statement will be :-
No. of red roses +No. of white roses ≥ 12
i.e.
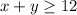
Also, Red roses cost $2.75 each and white roses cost $3.50 each and he wants to spend less than $35.
i.e. $2.75(No. of red roses)+$3.50(No. of white roses)≤ $35
i.e.
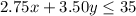
Now, From (1) and (2) the system of inequalities represents the situation :