Question

I need a solution

`2log_(x)25 - 3 log_(25)x = 1`

Answer 1

Given

`2log_x(25)-3log_(25)(x)=1`

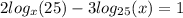
first, convert
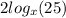
`2log_x(25)` to base 25 to match the other term.

`2log_x(25)`

`=2log_(25)(25)/log_(25)(x)`

`=2*1/log_(25)(x)`

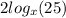
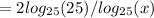
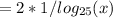
Substitute above identity into original equation:

`2/log_(25)(x)-3log_(25)(x)=1`

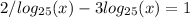
Use substiution
`u=log_(25)(x)`
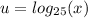
above equation becomes
2/u-3u=1
multiply by u and solve for u:

`3u^2+u-2=0`
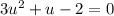
=> u=2/3 or u=-1

case A:. u=2/3 =>

`log_(25)(x)=2/3 => 25^(2/3)=x` =>

`x=25^(2/3) =8.54987973338348 (approx.)`

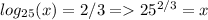
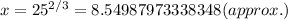
case B: u=-1 =>

`log_25(x)=-1`
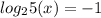
which does not give a real solution, so reject.

See graph below for confirmation of solution.