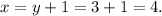Question

In a family, each brother has as many sisters as brothers, but each sister has twice as many brothers as she has sisters. How many brothers and how many sisters are there in this family?

Answer 1

4 brothers and 3 sisters

Explanation:

Let x be the number of brothers and y be the number of sisters in the family.

1. Each brother has x-1 brothers and y sisters. If each brother has as many sisters as brothers, then

`x-1=y.`

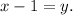
2. Each sister has y-1 sisters and x brothers. If each sister has twice as many brothers as she has sisters, then

`2(y-1)=x.`

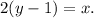
3. Solve the system of two equations:

`\left\{\begin{array}{l}x-1=y\\ \\2(y-1)=x\end{array}\right.\Rightarrow 2(y-1)-1=y,\\ \\2y-2-1=y,\\ \\2y-y=2+1,\\ \\y=3.`

Then

`x=y+1=3+1=4.`