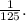Question

A quality inspector at a valve manufacturer randomly selects one valve from each batch of fifty valves to inspect for noncompliance. The first batch of fifty valves has five non-compliant ones. The second batch of fifty valves has four non-compliant valves. Find the probability that the inspector selects a non-compliant valve both times. A) 1/100 B) 1/125 C) 1/9 D) 9/50

Answer 1

The actual answer is 1/125......................................

Answer 2

The correct answer is B
`(1)/(125).`

Explanation:

Step 1

The fist step is to determine the probability of selecting a non-compliant valve from the first batch. Since there are 5 non-compliant valves in the batch out of 50 , we determine that the probability of finding a non-compliant valve is
`P(A)=(5)/(50).`

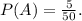
Step 2

The second step is to determine the probability of selecting a non-compliant valve from the second batch. Since there are 4 non-compliant valves in the batch out of 50 , we determine that the probability of finding a non-compliant valve is
`P(B)=(4)/(50).`

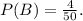
Step 3

The last step is to determine the probability of getting non-compliant valves both times. Since the two events are independent of each other, we find the probability by multiplying the probability of both events. The calculation is carried out as shown below,

`P(A)* P(B)=(5)/(50) *(4)/(50) =(20)/(2500) =(1)/(125).`

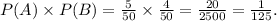
The probability of 2 non-compliant valves is
`(1)/(125).`