Answer: The slope of the line segment PQ is
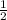 .
.
Step-by-step explanation:
From the given information it is observed that the and line segment have two end points P(-2,1) and Q(4,4).
The slope is he rate of change of one variable with respect to another variable.
If a line segment passing through the two points
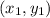 and
and
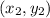 , then the slope of the line is defined as,
, then the slope of the line is defined as,
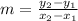
The two given points are P(-2,1) and Q(4,4).
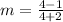
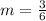
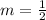
Therefore, the
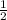 is the slope of the line segment PQ.
is the slope of the line segment PQ.