Answer:
(2, 2)
Explanation:
First we find the slope of the line through M and N. The coordinates of M are (2, 3) and the coordinates of N are (-3, 2). Using the formula for slope,
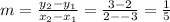
For a line to be perpendicular to a given line, the slopes would be negative reciprocals (opposite signs and the fraction is flipped). This makes the slope of the perpendicular line -5/1.
The coordinates of point K are (3, -3). Going down 5 units and right 1 unit would put it at (4, -8). Going backwards, up 5 units and left 1 unit would be (2, 2). Thus (2, 2) is the point we are looking for.