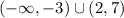Answer:
The solution is
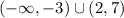
Explanation:
Given the inequality

we have to find the solution of the above inequality.

The solution is x=2, x=-3 for (x-2)(x+3)=0
The domain for the above inequality is

we use the number line rule for inequalities (first by making the coefficients of x positive then taking the roots on the number line and depending on the sign in the equation we start taking alternate signs and depending on the inequality take the desired region)
we get,