Answer:
it decreases by a factor of 16
Step-by-step explanation:
The intensity of a sound wave is inversely proportional to the square of the distance:
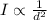
where d is the distance.
Let's call d the initial distance. In this problem, the distance is then quadrupled, so the new distance is d' = 4 d. Substituting in the formula, we see that the new intensity is:
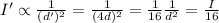
So, we see that the intensity has decreased by a factor 16.