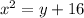Question

The relationship between two numbers is described below, where x represents the first number and y represents the second number. The square of the first number is equal to the sum of the second number and 16. The difference of 4 times the second number and 1 is equal to the first number multiplied by 7. Select the equations that form the system that models this situation. Then, select the solution(s) of the system. Equations Solutions y2 + 16 = x (2x)2 = y + 16 (1,15) (5,9) x2 = y + 16 7y - 1 = 4x (2,-12) (8,48) 1 - 4y = 7x 4y - 1 = 7x (4,-7) (9,3) NextReset

Answer 1

x^2=y+16

4y-1=7x

(5,9)

Answer 2

`x^2=y+16`

`4y-1=7x`

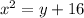
Explanation:

The condition says:

The square of first number is equal to the sum of the second number and 16:

Lets say that the first number is 'x' and the second number is 'y'. So the square of 'x' is
`x^2` and that is equal to the sum of second number i.e y and 16:

`x^2=y+16`

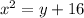
Second condition says that:

The difference of 4 times the second number and 1 is equal to the first number multiplied by 7:

4 times the second number is
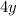`4y` and difference of 1 is:

`4y-1`

and this is equal to 7 times the first number:
`7* x`

`4y-1=7x`

So the two equations are:

`x^2=y+16`

`4y-1=7x`